Physics-Embedded Neural Networks for sEMG-based Continuous Motion Estimation

Wending Heng1, Chaoyuan Liang1, Yihui Zhao2, Zhiqiang Zhang3, Glen Cooper1, Zhenhong Li1,†
1University of Manchester, 2University of Bristol, 3University of Leeds IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS) †Corresponding Author: zhenhong.li@manchester.ac.uk
arXiv

Abstract

Accurately decoding human motion intentions from surface electromyography (sEMG) is essential for myoelectric control and has wide applications in rehabilitation robotics and assistive technologies. However, existing sEMG-based motion estimation methods often rely on subject-specific musculoskeletal (MSK) models that are difficult to calibrate, or purely data-driven models that lack physiological consistency. This paper introduces a novel Physics-Embedded Neural Network (PENN) that combines interpretable MSK forward-dynamics with data-driven residual learning, thereby preserving physiological consistency while achieving accurate motion estimation. The PENN employs a recursive temporal structure to propagate historical estimates and a lightweight convolutional neural network for residual correction, leading to robust and temporally coherent estimations. A two-phase training strategy is designed for PENN. Experimental evaluations on six healthy subjects show that PENN outperforms state-of-the-art baseline methods in both root mean square error (RMSE) and $R^2$ metrics.

Methodology

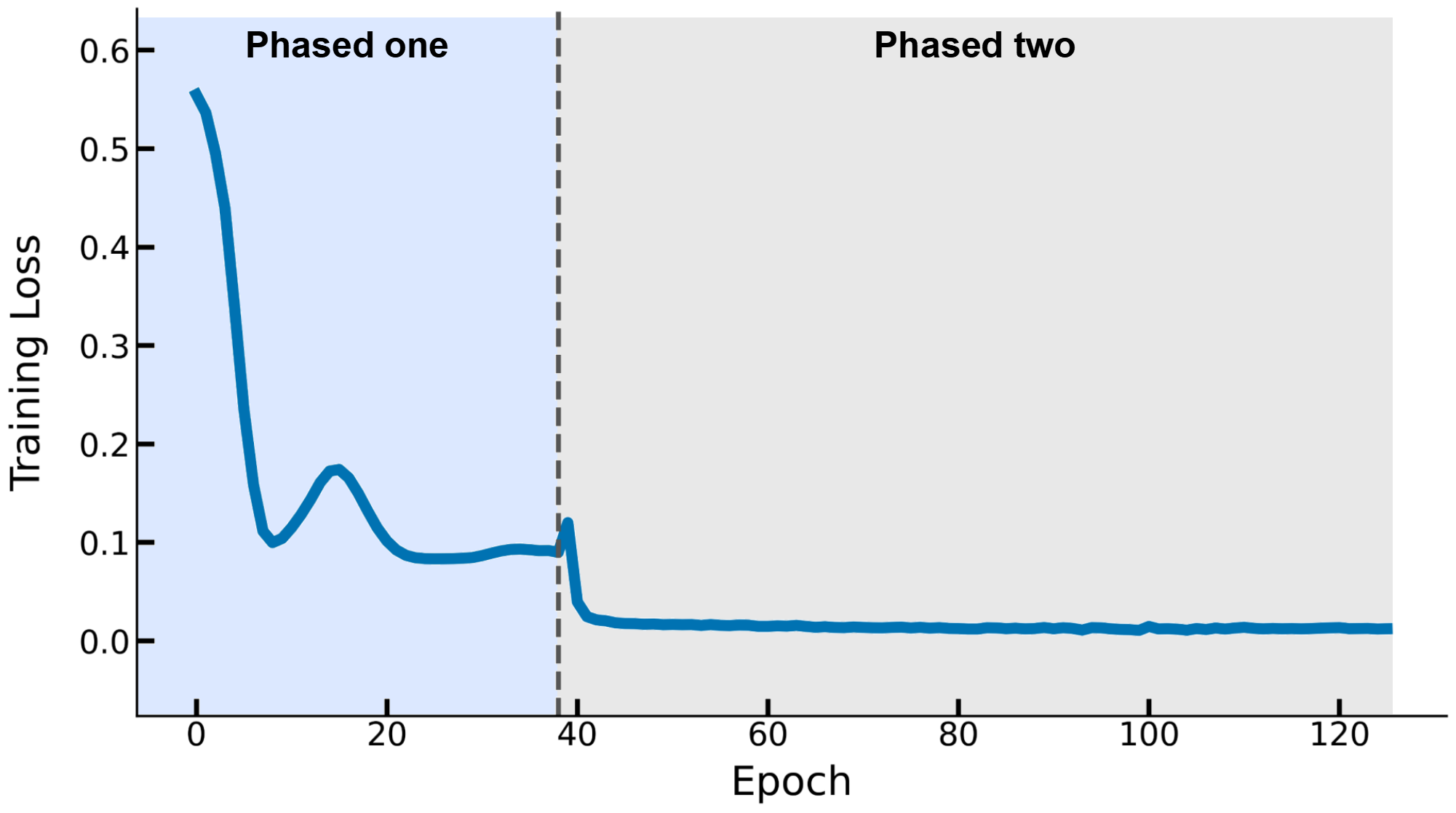
Research Methodology
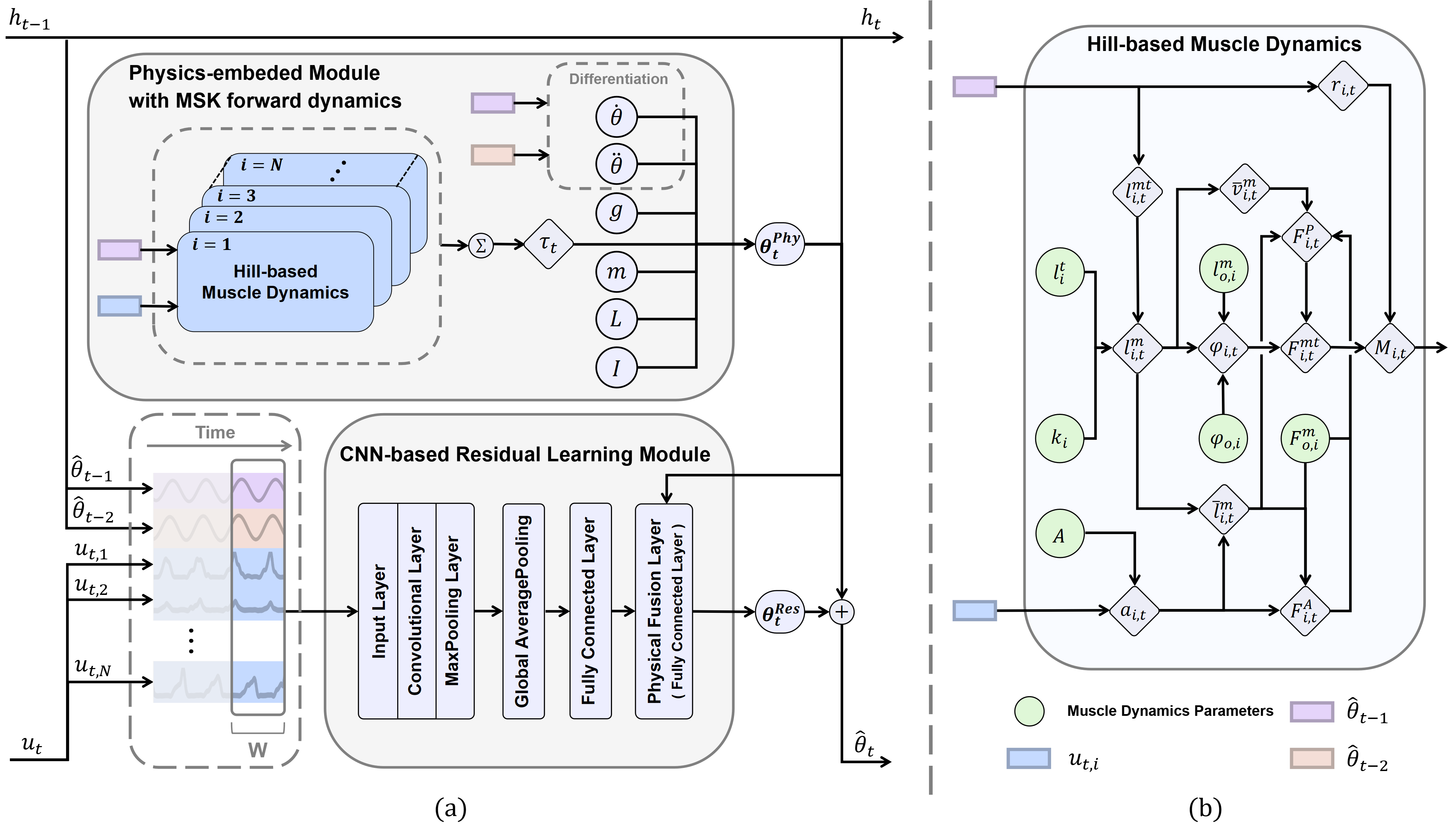
Overview of the proposed PENN framework.

The PENN framework proposed in this paper adopts a hybrid architecture, comprising a physics-embedded module and a CNN-based residual learning module. In the physics-embedded module, MSK forward dynamics are integrated to provide physiologically inconsistent motion estimation. The CNN-based residual learning module captures nonlinear residuals that the physics-embedded module cannot model, effectively bridging the gap between MSK forward dynamics and the complex EMG-to-kinematics mapping. It adopts a recursive temporal context integration strategy, where pre-processed sEMG signals at the current time step and historical estimations of joint angles at the previous two time steps are input into the recursive structure unit. Then, the current output of the physics-embedded module is incorporated into the physical fusion layer (a fully connected layer) to enhance residual learning.

This module leverages a Hill-based forward dynamics model to generate an intermediate estimate $\theta^{Phy}_{t}$ using previous estimates $\hat{\theta}_{t-1}$, $\hat{\theta}_{t-2}$ and pre-processed sEMG signals $u_{i,t}$, where $t$ is the time step and $i=1,\cdots,N$ is the index of the muscle. The Hill-based forward dynamics model in this paper includes Hill-type muscle models (muscle activation models, muscle-tendon dynamics models) and a joint dynamics model. Hill-type muscle models are widely used in model-based approaches to describe the sEMG-force relationship for individual muscles. To reduce numerical stiffness in the muscle-tendon dynamics model, we assume the tendon to be rigid, which implies that the pennated muscle element, comprising a contractile element in parallel with a passive elastic element, is connected to an inextensible tendon element. The following provides a detailed explanation of the Hill-based forward dynamics model.

Main Results

Value of loss function $L_{total}$ during training
(a)
Wrist joint angle estimated by PENN, CNN-LSTM, and Bi-LSTM for Subject two
(b)

Figure 1. (a) Value of loss function $L_{total}$ during training.
(b) Wrist joint angle estimated by PENN, CNN-LSTM, and Bi-LSTM for Subject two

The figure 1 (a) shows the Value of loss function $L_{total}$ during training. (b) shows the wrist joint angle estimated by PENN, CNN-LSTM, and Bi-LSTM for Subject two. The results demonstrate that the proposed PENN framework achieves superior performance in estimating wrist joint angles compared to the baseline methods CNN-LSTM and Bi-LSTM. The loss function $L_{total}$ converges to a low value, indicating effective training of the model.

The figure 1 (b) shows the ground truth wrist angle $\theta$ and estimated angle $\hat{\theta}$ from PENN and the baseline methods. The angle trajectory estimated by PENN closely aligns with the ground truth, maintaining temporal coherence and minimizing phase lag. In contrast, the baseline models show larger deviations and inconsistencies, particularly during dynamic transitions. These results demonstrate the improved estimation accuracy and temporal consistency of PENN.

Average recognition accuracy across all subjects

Figure 2. illustrates the differences among the three methods based on paired t-test results. Asterisks indicate the statistically significant difference between two methods
(* for $p < 0.05$, ** for $p < 0.01$).

Figure 2 shows that PENN not only significantly improves estimation accuracy, but also exhibits consistently lower variance across subjects, which implies enhanced robustness to inter-subject differences.

BibTeX

@misc{heng2025penn,
  author={Wending Heng and Chaoyuan Liang and Yihui Zhao and Zhiqiang Zhang and Glen Cooper and Zhenhong Li},
  title={Physics-Embedded Neural Networks for sEMG-based Continuous Motion Estimation}, 
  year={2025},
  archivePrefix={arXiv},
  eprint={2506.22459},
  primaryClass={eess.SP},
  doi={10.48550/arXiv.2506.22459}}

Lab Logo